FIR and IIR Filter

Contents
Reference vedio
Digital Filter Introduction and Overview
- Digital filter is huge part of DSP
- input signal represnted by a discreate time sequence (fixed sampling frequency, $f_{s}$)
- Nyquist frequency limit ($frac{f_{s}}{2}$)
FIR
1. FIR Filter Theory
- FIR: Finite Impulse Response
- It is defined by a finite number of coefficients (h) , and the output is acquired by convolution of the input signal with the impulse response.
- Fourier transform of the impulse response = frequency response of filter
- convolution in time domain = multiplication in frequency domain
FIR fomulas
- $y (output) = x (input) * h$
- $y[n] = \sum_{j =0}^{M - 1}h[j]~x[n-j]$ (discrete time)
- inpulse response length = M
2. FIR Filter Design
Rough Design procedure
- design the required frequency response
- inverse Fourier transform
- find the impulse response (h)
The Window-Sinc Method
$h(t) = \frac{1}{2\pi} \int_{\inf}^{-\inf} X(\omega)*e^{j \omega t} d\omega $
$h(t) = \frac{1}{2\pi} \int_{f_c}^{-f_c} 1*e^{j 2 \pi f t} df $
then we get sinc function
$h(t) = \frac{sin(2 \pi f_c t)}{\pi t}$
-
Problems
- Non-casual (t < 0, value != 0): solve by shifting response
- Infinite length: solve by truncating
- Continuous: solve by sampling
-
The output after shifting, truncating and sampling
- Problems
- Side-lobes: solve by multiplying impulse response by windowing function (smoothing)
Window-Sinc FIR Filter Design Procedure
- Choices When Designing FIR Filters
- Sampling frequency
- Filter length
- Frequency response, filter type: low-pass, high-pass, band-pass, band-stop
- Window function
- Time-domain properties: linear phase, minimum phase, maximum flatness
3. FIR Filter Software Implementation
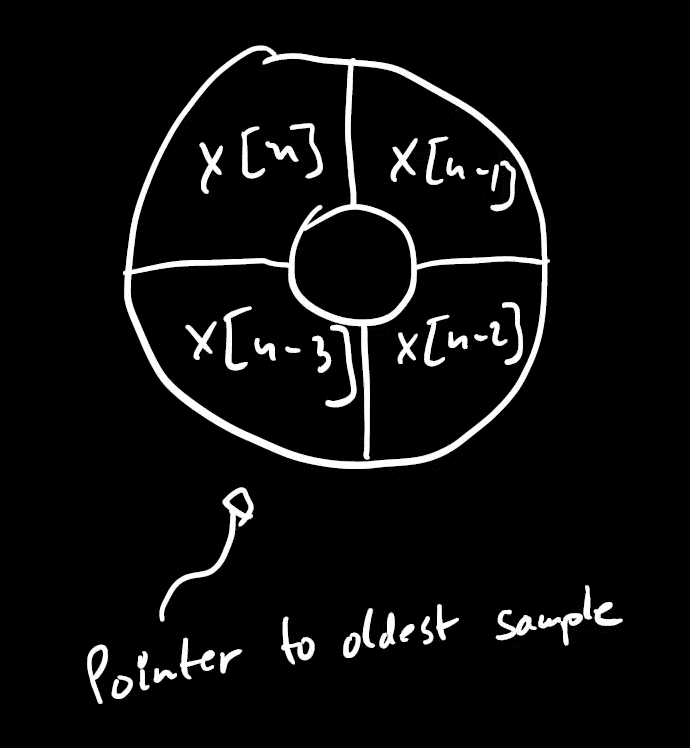
Convolution and Circular Buffers
- convolution formula: $y[n] = \Sigma_{j = 0}^{M - 1} h[j]x[n - j]$
- If we use a linear buffer, we need to shift the data every time we get a new sample
- We can solve this problem by using a circular buffer
Serial Oscilloscope Tool
IIR
1. IIR vs FIR
| IIR | FIR | |
|---|---|---|
| Impulse Response | Infinite | Finite |
| Performance | X | O |
| Speed | O | X |
| Stability | can be unstable | always stable |
2. IIR Filter Theory
- IIR: Infinite Impulse Response
- Recursive filter which use feedback to bypass a longer convolution
IIR fomulas
- $y[n] = \sum_{i = 0}^{A}a_i~x[n-i] + \sum_{j = 1}^{B}b_j~y[n-j]$ (discrete time)
- $a_i,~b_i$ are filter coefficients

3. IIR Filter Design
Design methods
- Online tools or Matlab
- Use standard types: Butterworth, Chebyshev, Elliptic
- Optimisation methods (minimise some cost function)
- Analogues prototypes + discretisation
- Z-transform
4. IIR Filter Software Implementation
SKIP